이하 글들은 (https://kdst.re.kr)에 게재한 글과 동일 저자가 작성한 글임을 밝힙니다.
이번에는 CVPR 2020에 Oral session에 발표된 논문인 Revisiting Knowledge Distillation via Label Smoothing Regularization을 리뷰하려고 합니다. 논문은 링크를 참조해주세요
Background
Geoffrey Hinton 이 2014년 NeurIPS에 발표한 Distilling the Knowledge in a Neural Network 이후로 분야가 개척되어왔습니다.
Knowledge Distillation에서 Hinton이 발표한 방식은 pretrained teacher model의 logits과 student모델의 logits의 soft-target을 구해서 KL Divergence를 취해서 서로 분포간의 거리를 좁히는 방식으로 학습이 진행되어 왔습니다.
$$ L=L_{CE}(y|x;\theta)+L_{KD}(y,y'|x;\theta_{stu},\theta_{teacher})$$
그 이후 많은 Knowledge Distillation Method(이하 KD)들이 발표되고 있으며, 기존의 logits(neural network output)들을 가지고 KD를 어떻게, 무엇을 하는 지에 대해서 연구가 진행되고 있습니다.
Knowledge Distillation에는 구성요소가 여러가지가 있는데, Knowledge 종류, learning scheme, architecture 등등이 있습니다. 간단히만 설명하자면, Knowledge 종류에는 logits을 활용한 response-based knowledge, intermediate layer output을 활용하는 feature-based knowledge, 그리고 instance를 활용한 relation-based knowledge가 존재합니다.
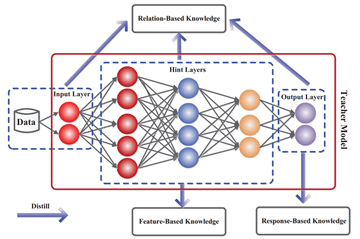
또한, learning scheme은 Distillation을 누구와 언제 하는지에 관한 것인데, pretrained model을 갖는 것은 offline KD, teacher와 student가 동시에 학습하는 것은 online KD, teacher와 student가 같은 것이 self KD라고 할 수 있습니다.

이중에서 논문은 response-based knowledge, 즉 logits을 활용하여 teacher와 student가 같은 self knowledge distillation에 대해서 집중적으로 다룰 예정입니다.
- Response based Knowledge Distillation
logits $z$ vector를 활용하여 $p(z_i,T)=exp(z_i/T)/{\sum_{j}exp(z_j/T)}$인 soft-target은 teacher로 부터 student에게 informative dark knowledge를 전달한다는 것이 일반적인 통념이었습니다.
하지만, 저자는 이러한 common belief에 대해서 혹시 regularization method중 하나인 label smoothing regularization과 유사하게 생겼다는 의문을 품고 2가지 실험을 구성하여 이를 검증해보려고 합니다. 만약 두 실험이 성립하는 경우, dark knowledge가 정보를 전달하기 보다는 그냥 label들을 정규화(regularize)하는 method중에 하나임을 실험적으로 증명할 수 있기 때문입니다.
1번째 실험은 student model로 사용되는 light model과 teacher model로 사용되는 deep model의 역할을 바꾸어 학습을 시켜보는 것입니다. (Reversed KD, Re-KD)
2번째 실험은 teacher model을 덜 학습시킨다음(low accuracy) student에게 knowledge transfer를 진행하는 것입니다. (Defective KD, De-KD)
Cifar100 data를 활용한 해당 Exploratory Experiment의 결과는 다음과 같습니다.
1번째 실험은 Re-KD와 일반적인 Normal KD의 결과 비교 입니다.

표를 보면 T->S 에서 Student의 성능향상이 뚜렷하게 높긴하지만, Re-KD에서 S->T에서의 학습 향상을 볼 수 있습니다.
2번째 실험은 De-KD의 결과입니다.

개인적으로는 이 실험결과가 엄청 놀라웠는데요. Teacher를 poorly-trained model로 구성하여 student를 학습시킨 결과 student가 눈에 띄게 증가하는 것을 확인할 수 있었기 때문입니다. 이를 통해서
실험 1의 Normal KD와 실험2의 De-KD를 비교해보면 대체로 Normal KD만큼은 아니지만 De-KD에서도 성능향상이 이루어진다는 사실을 확인할 수 있었고, 심지어는 ResNet50을 teacher로 활용하는 MobileNetV2를 학습시키는 경우, Normal KD보다 높은 성능을 보이기도 하는 등, 실제로 dark knowledge가 아니라 regularizer의 역할을 할 수도 있을 것 같다 라는 생각이 드는 실험이었습니다. 2번째 실험과 1번째 실험의 Normal KD를 같이 비교하지 않은점은 좀 아쉬웠습니다.
Motivation
이러한 실험적 확인 이후, 본 논문에서는 KD를 regularization method중에 하나인 Label Smoothing Regularization(LSR)과 유사하기 때문에 이를 수학적으로 유사함을 증명하려고하였습니다. Normal Classification에서 output distribution은 $p(k|x)=p(k)=softmax(z_k)=exp(z_k)/{\sum_{i=1}^{k}exp(z_i)}$ 를 사용하여 ground truth에 대해서 cross-entropy loss를 활용합니다.
$$H(q,p)=-\sum^{K}_{k=1}{q(k|x)log(p(k|x))}$$
Label Smoothing Regularization (LSR)에서는 cross-entropy loss에서 사용되는 ground truth q(k|x)를 바꾸어 q'(k|x)를 사용합니다. 정답 label을 확률 1로 보는 것보다 낮은 값을 선택한 후 남은 값을 다른 label에 분배하는 것입니다.u(k)=1/K로 uniform distribution입니다.
$$q'(k|x)=(1-a)q(k|x)+au(k)$$
Knowledge distillation에서의 loss function은 다음과 같습니다.($\tau$는 temperature)
$$L_{KD}=(1-a)H(q,p)+aD_{KL}(p^t_{\tau},p_{\tau}) $$
LSR에서의 loss function은 다음과 같습니다.
$$H(q,p)=-\sum^{K}_{k=1}{q'(k)log(p(k))}$$
$$L_{LS}=(1-a)H(q,p)+aD_{KL}(u,p)$$
이 두식을 정리해서 풀면 다음과 같이 굉장히 유사한 식으로 구성이 됩니다.
q'(k) in LSR: $q'(k)=(1-a)q(k|x)+au(k)$
q'(k) in KD: $q'(k)=(1-a)q(k|x)+ap^{t}_{\tau}(k) when \tau =1$
이를 통해서 $\tau$를 조정하면 $p^{t}_{\tau}(k)$가 $u(k)$와 유사하기 때문에 이를 저자는 KD가 LSR의 특별한 케이스로 보고 있습니다. 왜냐하면 temperature $\tau$가 커지면 커질 수록 유사한 값이 나오기 때문입니다.
이러한 사실들을 기반으로 그렇다면 KD가 regularizer의 한 종류로 볼 수 있기 때문에 이를 통해서 Teacher-free Knowledge Distillation이라는 새로운 방법론을 제시합니다.
Proposed Method
1) Teacher-free Knowledge Distillation (self-training)
간단한 pipeline은 student를 학습시킨 후, 그 student model을 복사하여 student model을 teacher로 사용하는 방법입니다. 아래 사진에서 teacher model로 student 자신을 사용하는 방법입니다. 나머지는 Normal KD와 동일합니다. 개인적으로는 이 부분은 2015년 이후 한 번쯤은 생각해볼 방법론이라 간단하게 넘어가겠습니다.
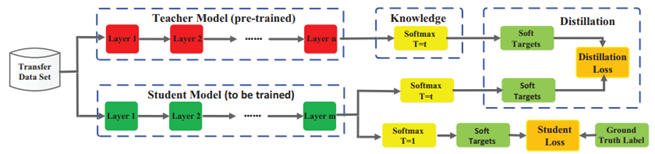
2) Teacher-free Knowledge Distillation (self-regularization)
개인적으로는 이 부분이 엄청 많이 추가가 된 것은 아니지만 성능 향상이 나름 인상적이었습니다. LSR의 방식을 도입한 후, 해당 label을 soft-target을 취해서 student의 logits과 KD Loss를 취하는 방식입니다. 한마디로 ground truth에 대해서 fake teacher처럼 soft를 취해서 KD를 진행한다는 것이죠.
KD에서 사용하는 fake teacher에 대한 output distribution은 다음과 같습니다.
$$ p^{d}(k)=\begin{cases}a &if k = c \\ {1-a}/{k-1} & if k \neq c \end{cases} $$
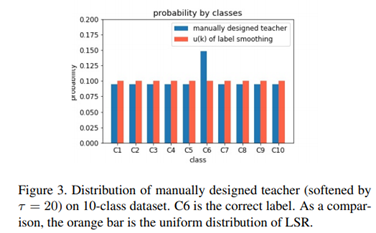
Pipeline을 보기 쉽게 설명하면 다음과 같습니다.

Teacher를 쓰는 것이 아니라 가상으로 두고 target값을 label smoothing(by softmax with temperature)하여 KD Loss를 취할 수 있게 하는 것이 이 논문의 핵심 방법론이라고 볼 수 있습니다.
Experiment
cifar100에 대한 self-training Tf-KD의 결과는 다음과 같습니다.

사실 이 부분은 더 큰 모델을 사용할 필요 없이 Tf-KD_self가 유사하거나 높은 성능을 냄을 확인함으로서 더이상 big teacher가 필요 없다는 데 의의가 있는 실험결과입니다. 통념적으로 믿어온 잘 가르치는 선생님은 친구이기도 하다는 것과 같습니다.
두번째 Tf-KD_reg 방법에 대한 실험 결과는 다음과 같습니다.

Normal KD에 대해서 유사한 성능을 보여주고 있고, LSR에 대해서는 더 좋은 성능을 통해 Soft-target을 취했을 때 성능 향상에 도움이 됨을 확인할 수 있습니다. 이 방법의 의의는 선생님 조차도 없이 스스로 distillation을 통해 성능 향상을 꾀할 수 있다는 것을 확인하였고, 엄청 큰 모델을 스스로 학습시킬 때에도 자유롭게 사용가능하다는 점을 생각해보면 의미있는 실험결과임을 알 수 있습니다.
Conclusion
결론은 Dark Knowledge라고 부르는 부분은 사실 Regularization Term으로 볼 수 있다 라고 말하고 있습니다. 이를 통해서 스스로 distillation 하는 self-distillation이 teacher-student관계가 존재하는 learning scheme만큼의 성능을 보여줄 수 있다는 것을 실험, 수식으로 설명한 강력한 논문이라고 생각합니다. 하지만, De-KD에서 15%의 accuracy를 갖는 ResNet을 teacher로 하는 결과와 Normal KD와 비교해볼 때, 눈에 띄게 성능저하가 존재하는 경우가 있다는 점을 고려해보면 Dark Knowledge가 존재할 수 있지 않을까? 라는 생각이 들었습니다.
자세한 내용은 논문을 참조하시거나 댓글로 남겨주시기 바랍니다.




댓글