이번에는 NIPS 2017 Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments을 리뷰하려고 합니다. 자세한 내용은 논문을 참조해주세요
Introduction & Background
강화학습, RL이 발전함에 따라서 더 복잡한 task를 다루어야 했고, 단순한 작업이라고 착각했던 로봇의 관절 움직임 같은 것들을 제어하는 데에 있어서 Multi-agent RL을 통해서 진행하는데에 어려움이 있어왔습니다.
Multi-agent reinforcement learning을 다루는데에 있어서 기존의 전통적인 방법들에는 다음과 같은 문제들이 있습니다.
1. Q-learning
기본적으로 Q-learning은 어떤 state $S$에서 action $a$에 대한 value를 더 높이는 방향으로 최적화하는 방법론을 의미합니다. 더 높은 Q를 선택할수록 더 좋은 결과를 가져올 수 있을 것이기 때문입니다.
$$Q^{\pi}(s,a)=E[R|s^t=s,a^t=a]$$
$$ Q^{\pi}(s,a)=E_{s'}[r(s,a)+\gamma E_{a'~\pi}[Q^\pi [s',a']]$$
Mult-agent에서는 action을 선택하는 policy가 agent 각각의 update에 따라서 변화하기 때문에 agent에서 update를 진행하면 p(s'|s,a)의 분포가 non-stationary 해져서 학습이 어렵다는 단점이 있었습니다. 또한, Off-policy를 사용하는 경우 past experience replay를 직접 사용할 경우, 안좋은 학습의 경험도 가져다가 사용할 수 있으므로 learning이 stable하지 않다는 단점이 있습니다.
- DQN (Deep Q Learning)
Q function의 parameter $\theta$을 최적화하여 target Q function에 대해 최적화하는 학습 방법론이며, performance의 stabilize를 위해 experience replay $D$를 활용합니다. 직접적인 multi-agent settting을 적용하면, environment가 Markov가정을 침해하여 agent update로부터 nonstationary해집니다.
2. Policy Gradient
기본적으로 policy gradient는 action을 선택할 때, expected return $R$을 최대화하는 방향으로 update를 하려고 합니다. $J_\theta=E_{s~p^\pi,a~\pi_\theta}[R]$, return을 누적하여 적용하는 경우 $R=\nabla_\theta log\pi_\theta(a|s)Q^\pi (s,a)]$로서 REINFORCE 알고리즘으로 사용할 수 있습니다.
하지만 $Q$와 $\pi$를 학습에 사용하면 true Q function을 approximation하는 actor-critic algorithm으로 발전하였습니다. 그중에서 Deterministic policy $\mu : S->A$를 사용하는 경우, Deterministic Policy Gradient(DPG) 알고리즘으로 발전하게 되었습니다.
하지만, 이러한 알고리즘 또한 Agent가 늘어남에 따라 action을 1과 0으로 부여하고 모든 agent들의 행동이 1인 경우는 엄청나게 줄어들고 update하는 gradient가 최적의 방향으로 가능 확률이 지나치게 낮아진다는 단점이 있습니다.
3. Competitive Environment
MARL알고리즘은 Reward의 특성상 cooperative에 집중해서 만들어진 경우가 많았습니다. 하지만, agent간 경쟁하는 상황(adversarial training) 즉, reward의 sum이 0이 되게 하는 상황에서 optimizing이 수렴하지 않거나 instability를 보이는 경향이 보였습니다.
Method
MARL의 적용을 위한 제한을 살펴보면
1) 학습된 policy는 execution에서 local information만 사용 가능하다. (Communication이 불가능한 경우도 산정해야 한다.)
2) A differentiable model of the environment dynamics를 가정해선 안된다. 모든 상황 (cooperative, competitive, mixed)를 가정해야 한다.
3) 어떤 agent에게 특정한 communication 구조가 형성되어있다고 가정하면 안된다. ( 1)과 같은 맥락입니다.)
위와 같은 제한을 이 논문에서는 다음과 같은 방법으로 다룬다고 나와있습니다.
Framework상에서 centralized training을 하고, decentralized execution을 진행(CTDE)하면 실행시에 communication의 제약 없이도 동작할 수 있다고 말하고 있습니다. 만약 그렇게 되면 policy는 Q value 연산시에 모든 agent의 action을 사용하여 유용한 정보를 담고 update를 할 수 있습니다. 또한, agent의 모든 policy에 따른 action을 Q function approximation에 사용가능 하므로 non-stationary함을 보완할 수 있다고 합니다.

1)에서 언급한 다른 agent의 policy를 관찰할 수 없기 때문에 agent $i$가 다른 agent들 $j \in J$의 policy를 approximate하여 예측된 action을 기반으로 Q value loss를 update를 하게 됩니다.
이때 예측된 policy는 $\hat{\mu}_{\varphi^{j}_{i}}$로서 log probability와 regularization term을 통해 update가 되게 됩니다.

그렇게 구해진 $\hat{\mu_{\varphi^{j}_{i}}}$로 centralized $Q_i$를 업데이트하게 됩니다.

DDPG와 이 식이 다른 점은 DDPG는 next action에 대해서 max Q로 sampling하여 구한다는 점입니다. 하지만 approximated policies를 통해 각 agent의 action을 예측하여 활용한다는 점이 다른 점입니다.
Suggestion of improvement (Agents with policy ensemble)
앞서 언급한 adversarial situation(competitive environment)에서 adversary는 다양한 전략으로 agents를 상대할 수도 있을 것입니다. 만약 한 policy에 대해서만 학습한다면 overfit될 위험이 존재합니다. 그래서 agent에게 sub-policy(ensemble)을 학습시킨다면 전략의 변화에 robust해질 것이라고 저자는 말하고 있습니다. 각 episode에서 random하게 sub-policy를 선택하여 학습시키며, sub-policy $\mu^{(k)}_i$는 각 replay buffer $D^{(k)}_i$ 에 유지해서 이를 활용하여 off-policy로 update를 다음과 같이 하게됩니다.

Experiments
- Explanation of environments
본 논문에서는 cooperative, competitive, mixed 등등의 다양한 environment에서 실험하여 결과를 증명합니다. 다음은 환경들에 대한 일부 설명입니다.
1) Cooperative Communication
Speaker랑 listener로 구성되며, listener가 특정 색을 찾아 가는 게임입니다. Listener의 reward는 정확한 특정 색의 위치와의 거리를 받습니다. Speaker의 경우, listener의 motion기반으로 color를 출력하는 output을 학습합니다.
2) Cooperative Navigation
Agent는 다른 agent들과 landmark의 상대적 위치를 갖습니다. 목표는 서로 부딛히지 않고, 모든 landmark를 점령하는 것입니다.

3) Predator-Prey
N개의 cooperating agent들은 adversary를 장애물을 피해서 쫓는 task입니다. 만약 agent가 adversary에 충돌하면 agent가 보상을 받고 adversary는 패널티를 부여받습니다.
4) Physical Deception
N개의 cooperative agent들은 single target landmark를 도달하는 task입니다. Adversary도 동일한 목표를 가지므로 agent들은 협력해서 adversary를 속이면서 목표에 도달하게 하는 것입니다.
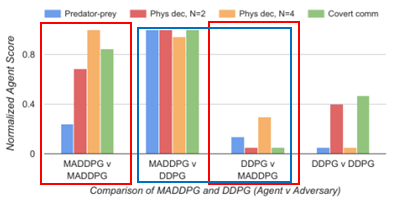
- Comparison between MADDPG and DDPG
Adversarial environment에서 MADDPG agents가 DDPG agent보다 성능이 더 높게 나오는 것을 확인할 수 있었습니다.(red)
DDPG를 cooperative agents로 사용할 때와 MADDPG를 cooperative agents로 사용할 때, adversary로 각각 MADDPG와 DDPG를 사용하여 비교하였을 때, MADDPG가 항상 성능이 높음을 짐작할 수 있는 그래프였습니다.
이러한 결과를 바탕으로 decentralized method들과 MADDPG를 cooperative communication task에 대해서 비교하였습니다. 아래의 그래프를 보면 MADDPG만 학습에 성공한 것을 알 수 있습니다. Cooperative communication에서는 서로의 action을 예측하지 않기 때문입니다. Assumption failure로 인해서 traditional method는 학습하기 어렵기 때문입니다. Speaker의 경우, 옳게 말해도 penalty를 받기 때문에 학습이 더 어렵다는 사실을 알 수 있습니다.

- Ensemble policy의 효과에 관한 experiment
앞서 다양한 strategies를 가진 adversary에 대응하기 위해서 ensemble policy를 도입했을 때 효과적일 수 있음에 대해서 method에서 제시하였습니다. 이러한 증명 실험으로 진행하였을 때, ensemble policy가 항상 single에 대해서 나은 결과를 보여주었습니다.

- Other agents의 policy를 approximation을 하는 것의 효과에 관한 experiment
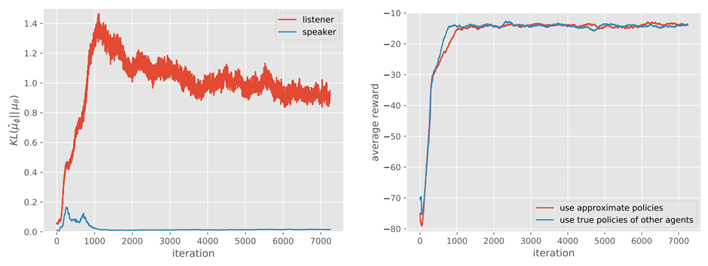
Learning centralized Q function을 통해서 $i$ agent기준 other agents $j \in J$의 policies 을 학습하는데, 이를 true policy (실제 agents $j \in J$)와 비교하여 KL divergence를 통해 비교하는 것을 통해 얼마나 유사한지 확인하여 이러한 approximation이 agent에 영향을 주는 것을 확인하였습니다.
Conclusion
Centralized Q learning을 통해서 다른 agent의 policy를 예측함으로써, execution할 때 영향을 받아 행동할 수 있도록 하는 MARL 알고리즘입니다. 하지만 agent가 중간에 사라진다거나 생성될 때에 대한 부분의 대처가 약간 아쉬웠습니다. 하지만, 많은 multi-agent task에서 generalize하기 좋은 알고리즘이라는 점에서 contribution이 있는 것 같습니다.
또, 위의 listener를 확인했을 때, listener의 KL divergence가 학습이 수렴함에 따라 증가했는데 이에 대한 해석이 없어 아쉬웠습니다. 이러한 점을 들어서 approximation에 대한 효과라고 볼 수 있는지 궁금했습니다.
자세한 내용은 논문을 참조하시거나 댓글로 남겨주시기 바랍니다.




댓글