이번에는 CVPR2020에 oral paper로 accept 된 Local Context Normalization: Revisiting Local Normaliztion을 리뷰하려고 합니다. 자세한 내용은 원문을 참고해주세요.
Introduction
Batch Normalization은 빼고 나누는 feature normalization을 통해서 deep learning architecture에서 많이 사용되어왔습니다. 특히, Batch Norm이 처음에는 covariate shift로 인해서 좋을 것이라고 예측했으나, 최근에는 Batch Norm(BN)이 optimization land scape를 평탄화함으로 써 학습의 수렴에 기여를 했음이 밝혀졌습니다. 하지만 본 논문에서 제시한 단점으로
1) small batch size는 model performance에 영향을 주는데 mean과 variance가 feature를 normalization을 진행하면서 full batch 의 statistics를 반영하지 못하는 문제가 존재합니다.
2) batch는 inference할 때, 존재하지 않기 때문에 mean과 variance가 pre-computed가 되어 사용됩니다. 이는 target data distribution의 변화가 model의 original training set에 맞게 조정된 값들에 영향을 받아 문제를 일으킬 수 있다는 것입니다. [1]
이런 문제들을 해결하기 위해서 나온 것이 Group Norm입니다. (GN)
GN은 channel을 group들로 나누어서 feature들을 각 group의 statistics에 맞게 normalization을 진행한다는 것이 특징입니다. Group Norm은 batch dimension에 대해서 normalization을 하지 않기 때문에 영향을 받아 batch size가 작아질 때 성능이 떨어지는 문제점이 발생하지 않습니다. 물론 batch size가 작을 때 Batch Norm과 경쟁 가능한 성능을 보여주었지만, GN은 segmentation과 video classification과 같이 애초에 batch size에 작을 때만 사용하였고, batch size가 클 때는 GN은 여전히 BN보다 성능이 낮았습니다.
Batch Norm, Group Norm, Instance Norm 그리고 Layer Norm은 모두 전역적 normalization을 시행합니다. (여기서 전역은 모든 value in channel을 의미하지, mini-batch를 coverage함을 의미하지 않습니다.) 하지만 spatial information에 대해서는 그렇게 사용하지 않고 모든 한 개의 channel은 그냥 normalization됩니다. 아래의 사진처럼 H,W에 대해서 모든 값이 같이 normalization됩니다.

앞이 말한 문제들을 intuition으로 본 논문에선 Local Context Normalization을 normalization layer로서 제안합니다. LCN은 local context가 존재하는 이웃끼리 normalization된 statistics를 정확하게 가져가는데 이점이 있다 라고 얘기하고 있습니다. 이는 contrast normalization approach라는 human vision system으로 부터 motivation되었다고 합니다.
LCN은 이전에 normalization method를 모두 능가하는 성능을 보여준다고 하고 이를 실험적으로 증명한다고 합니다.
Group Norm에서 문제였던, 모든 spatial dimension을 normalization함으로써 조금만 pixel의 shift가 존재하면 굉장히 prediction에 어려움을 겪었다고 합니다. 그래서 GN으로 fine-tuning을 하는 것이 굉장히 안좋았다고 얘기하고 있습니다. LCN은 이러한 부분의 문제를 local context만 봄으로써 해결하고 있다고 합니다.
Related Work
본 게시글에서는 contrast enhancement에 대해서만 간단하게 다루겠습니다.
Contrast는 일반적으로 image에 되게 다양하게 사용되는 개념이고, 'contrast enhancement'는 뚜렷하지 않은 이미지의 contrast를 높이거나 뚜렷한 이미지는 그대로 고정시키는 기법입니다. 이는 많이 사용되지는 않았지만, 사람이 어떤 특징적인 것을(강조되는 것을) 보았을 때 기억을 잘한다는 점을 사용해서 LCN에서도 활용하고자 했습니다. LCN도 local similarities를 강조하고 intensity information을 잘 보존한다는 특징이 있습니다. Computer vision 관점에서 보면 inputi image 를 pre-process에 사용하는 경우가 있습니다. 본 논문에서는 유사한 방식으로 input에서가 아닌 neural network 내부에서 사용하는 방식이라고 할 수 있습니다.
Method
Global Normalization 방법론들에는 BN, LN, IN, GN 이 있고, 이는 feature map의 각 채널의 full chape를 보는 것을 의미합니다.
2D이미지의 경우 가 원하는 모양의 vector가 됩니다.
BN은 (B,H,W)에 대해 normalization
LN는 (C,H,W)에 대해 normalization
IN은 (H,W)에 대해 normalization
GN (G,H,W) 에 대해 normalization, where G < C
모든 global normalization은 각 channel에 대해서 feature들을 보상하기 위해서 affine transform을 취합니다.
LCN은 어떻게 보면 GN에서 channel에 대한 그룹 이외에도 width와 height에 대한 group이 생기는 거라고 생각하면 됩니다. 대신에 모두 hyper-parameter로 맞게 조정을 하면 된다고 합니다.


이런 방식으로 구현하면서 구현적인 issue가 생길 수 있는데, dilated convolution과 integral trick, summed area table algorithm을 사용해서 area에 대한 mean 과 variance를 효과적으로 풀어냈다고 한다. 이 부분을 좀 신기하게 봐서 자세하게 설명을 하자면,
우선 psuedo-code를 보면서 이해해보자.

처음에 를 보면 integral image of x에서 이미지 x에 대해서 (B,C,H,W)라고 하면 H와 W차원에 대해서 cumulative sum(Integral)을 먼저 진행한다. (갑자기? 라고 하면 따라와 보자)
이렇게 되면 이미지는 누적 그래프 처럼 값이 끝으로 갈수록 커지는데 이런 상황에서 논문에서 언급한 summed area table algorithm을 사용하면 각 group(GN의 group말고 LCN에서의 group) 에 대해서 평균과 분산을 구하기 굉장히 쉬워진다.
- Summed table algorithm (Reference: Wikipedia)
Summed table algorithm은 자료구조의 한 형태라고 보면 되고, 어떤 구역에 대해서 합과 같은 연산을 구하기 쉬워지는 알고리즘이라고 생각하면 된다. 아래 그림을 보면 1.에서 네모나게 그려져 있는 부분들이 우리의 group이라고 생각해보자. 그 중에서 보라색 부분을 생각해보면 15,16,14,28,27,11 이렇게 를 평균을 구할려면 먼저 합을 구해야 한다. 이때 cumulative sum을 우리가 갖는 feature map에 진행하면 2번과 같이 나온다.
이때, 우리가 원하는 그룹 크기의 index를 2. 그림의 index처럼 생긴 '원'을 [ [1,-1], [-1,1] ]연산을 convolution net을 통과하듯이 해당지점을 콕 집어서 연산을 하면 보라색 group의 값의 합을 얻을 수 있게 된다. 그러고 group크기로 나누면 평균 를 얻을 수 있게 되는 것이다. 그렇다면 '원'을 콕 어떻게 집을 수 있을까?

이때 앞서말한 dilation convolution이라는 기법이 사용된다. Dilation convolution은 segmentation에서 넓은 spatial information을 real time에 연산하고 싶을 때 사용하는 기법으로 아래의 그림을 보면 이해가 된다. [3]

Dilation convolution은 5x5커널의 연산을 모두 수행하지 않고 kernel weight를 0으로 채워서 3x3값만을 보지만, 5x5의 공간 정보를 보는 것과 같은 효과를 일으킨다.
Dilation convolution에서 dilation rate가 얼마나 많은 칸을 건너 뛸지인데 위 이미지는 dilation rate 2로 2칸 건너 연산한다. (우리가 쓰는 conv2d는 dilation rate가 1이다!)
이렇게 하면 LCN의 group의 크기로 dilation rate를 정해주면, summed area table algorithm으로 mean variance를 구할 수 있게 된다. 이렇게 구함으로써 구현이슈 또한 쉽게 해결했다고 합니다.
Experimental Results
object detection, (semantic, instance) segmentation 에 대해서 진행했습니다.
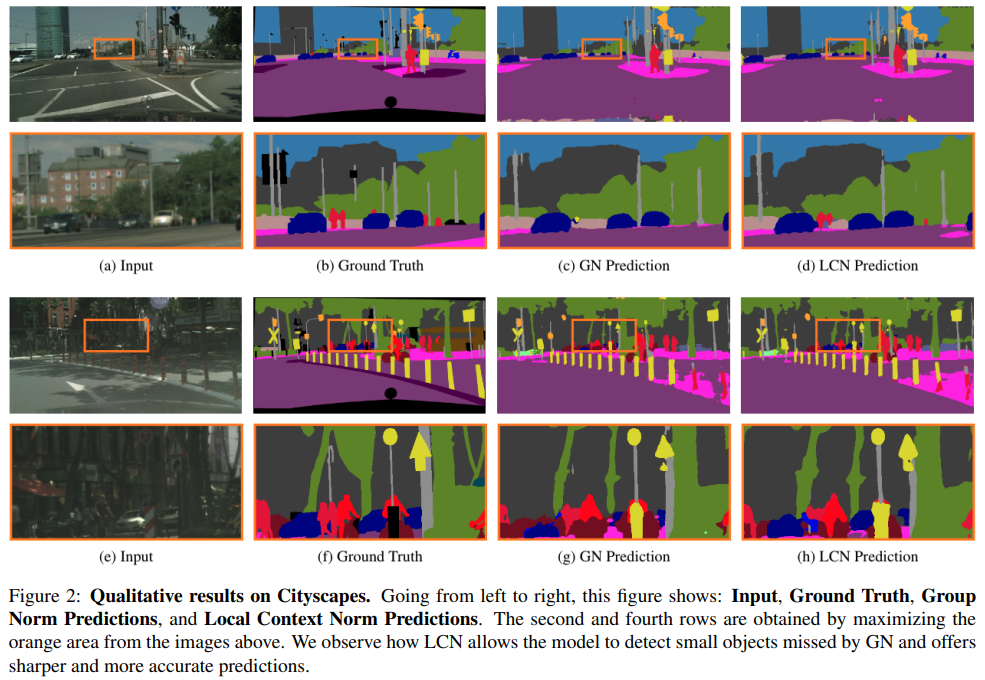
local context에 집중하게 되면서 좀 더 뚜렷한 윤과을 잡아내면서 prediction이 GN에 비해서 가능했다고 합니다.
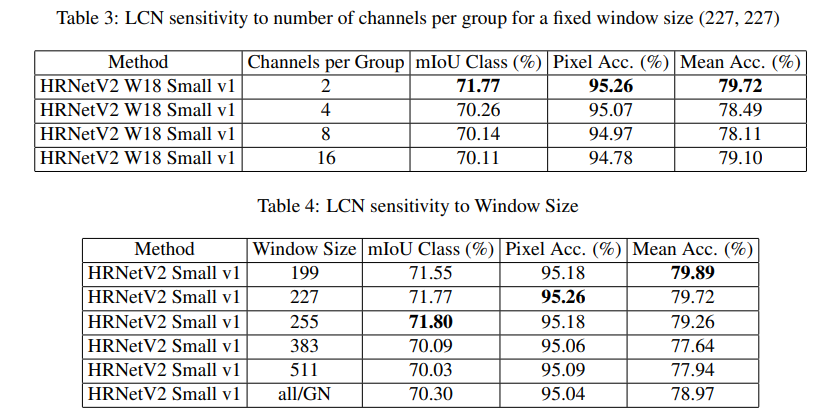
저는 hyper-parameter sensitivity에 결과를 좀 더 집중했는데,
흥미로운점은 window size가 생각보다 꽤 커야한다는 점이었고, channel에 대한 group은 채널수가 작을 수록 성능이 더 좋았다는 점입니다. ( 굳이 channel에 group을..? 지어야 하는가가 궁금했습니다.)
이상입니다.
Reference
[1] Learning multiple visual domains with residual adapters., Sylvestre-Alvise Rebuffi et al., NeurIPS 2017.
[2] https://en.wikipedia.org/wiki/Summed-area_table
Summed-area table - Wikipedia
Using a summed-area table (2.) of an order-6 magic square (1.) to sum up a subrectangle of its values; each coloured spot highlights the sum inside the rectangle of that colour. A summed-area table is a data structure and algorithm for quickly and efficien
en.wikipedia.org
[3] https://github.com/vdumoulin/conv_arithmetic/blob/master/README.md




댓글